Logistic 回归的 Loss 函数为什么长成那个样子?
一般人大概都能想得到,Logistic 回归的 Loss 函数应该是下面的样子。
(以下是正常的版本。)
这里 $1/2$ 是为了求导后方便计算的系数,不重要。
$n$ 是样本数量。
括号里面就是分错的部分了,很容易理解。
但实际上,它的 Loss 函数长成了这个样子:
为什么呢?
答案是:保证凸性。
第一个 Loss 函数不是凸函数,而取过了 $-\log$ 并且分段以后就变成凸函数了。
凸优化 及 梯度下降法
几乎每一个机器学习问题都是一个优化问题。
而在所有优化问题当中,有一类优化问题是人们非常关心的,并希望每一个优化问题都能转化为这样的优化问题的,那就是凸优化问题(convex optimization)。
一类常见的凸优化问题就是目标函数是凸函数,并且边界条件是仿射集的优化问题。如:支持向量机(SVM) 、 感知机(Perceptron)等等。
为什么要研究凸优化呢?因为凸函数有一个优点——全局最小值。
它可以让人们明确一个信念,即:所研究的问题一定是可学习的,而且一定在全局有一个固定结果,并不会踩到某个局部极值从而达不到最优。
那么如何求得这个最值呢,一般的方法是利用梯度下降法(gradient descent,GD)。
由于凸函数有一个一阶条件:$f(y) \ge f(x) + \nabla f(x)^{\mathsf{T}}(y-x)$ ,所以我们很容易看到,沿着目标函数 $f$ 的梯度方向一直下降的话(其实是梯度方向的反向,因为要下降),终究会像从沙滩上滑下一般到达最小值。
(顺便一说凸函数还有一个二阶条件:$\nabla^{2}f(x) \ge 0$ 。)
那么,问题来了,如果目标函数不是光滑的怎么办?
比如 $y=|x|$ ,这很明显是一个凸锥。
再比如,神经网络(neural net,NN)中最常见的激活函数(activation Function):ReLU,这也是一个凸锥。
解决方法是提出次梯度(subgradient)的概念。
所谓次梯度,是一个很像梯度的,但是是个常量的 $g$ ,它满足:$f(y) \ge f(x) + g^{\mathsf{T}}(y-x)$ 。
形式上是不是和凸函数的一阶条件很像?因此我们实际上是找了一个很像梯度的替代品。
例如:在 $y=|x|$ 的条件下,我们可以把原点的次梯度定义为 0。在ReLU的条件下,我们把原点的次梯度定义为 $1/2$ 等等。
样子如下图中的红线的斜率:
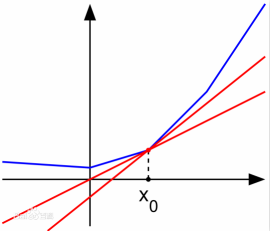
(原图来自 百度百科:次导数)
扩展:Softmax 模型的 Loss 函数—— Log-Sum-Exp 函数
这里就不给出函数的形式了,大家请自行 wiki。
总之来说,是 Logistic 模型的 Loss 函数的高阶扩展。也是一个带有一堆 $\log$ 、$\exp$ 还要求加和的式子。
它的凸性可以证明如下:
首先,我们考虑函数 $f(x) = \log (\sum \alpha_{i} e^{x_{i}})$ ,我们证明它是凸的。然后根据凸函数的性质 Affine composition 来导出 Log-Sum-Exp 函数是凸的。
(Affine composition 指的是:$f(x)$ 是凸的 $\Leftrightarrow f(Ax+b)$ 也是凸的,即对自变量做仿射变换不影响凸性。)
考虑:
显而易见,$\nabla_{i}^{2} f$ 是对角优势矩阵(diagonally dominant matrix)。
(对角优势矩阵:对矩阵 $A$ 的所有对角元,有 $A_{ii} \ge \sum_{i \ne j} |A_{ij}|$ 。)
因此,$\nabla_{i}^{2} f$ 是半正定的(positive semidefinite matrix,p.s.d)。
所以得到 Log-Sum-Exp 函数是凸的。