说一说核方法（二）——数学角度简介（掉粉文）

泛函分析（functional analysis）主要研究的是函数空间（function space），也就是说这个空间中所有的点（元素）都是函数。

先介绍几个概念，我们暂时只讨论由线性空间发展出来的概念，因为线性空间有很多很好的性质。

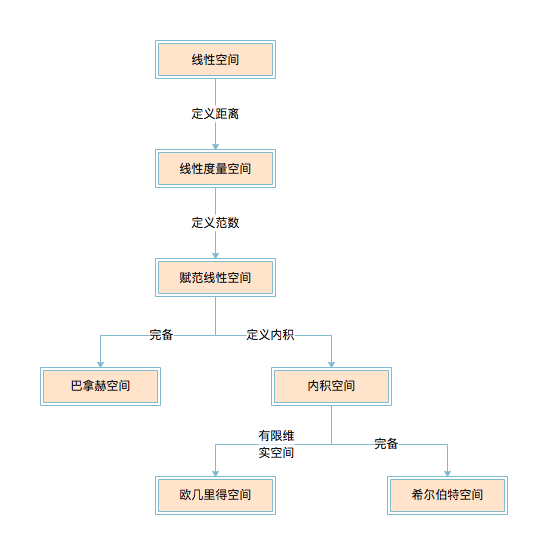
线性空间

线性空间（linear space）是定义了数乘和加法的空间。所以我们可以找到一组基底（basis），然后通过这一组基底的线性组合来得到空间中的所有点。
举个例子，二次函数空间，基底就可以定义为 $\lbrace 1, x, x^{2} \rbrace$ ，这个空间中任意的函数 $f(x)$ 都可以表示为 $f(x) = \alpha_{1} \cdot 1 + \alpha_{2} \cdot x + \alpha_{3} \cdot x^{2}$ ，所以我们可以说 $f(x)$ 在这组基底下的坐标是 $\lbrace \alpha_{1}, \alpha_{2}, \alpha_{3} \rbrace$ 。（请自行想象三维空间中，三个维度的坐标不是 $\lbrace x, y, z \rbrace$ 。）
当然基底也可以定义为 $\lbrace 1, x+1, (x+1)^{2} \rbrace$ ，但是计算上会增大难度。所以我们可以看出来基底只要是线性不相关的就行了。那么基底中有 $n$ 个元素的话，我们就叫这个空间是 $n$ 维的。
一般来讲，选用的基底都是正交基（orthogonal basis），也就是基底中的任意两个元素的内积为 0。

线性度量空间

线性度量空间（metric linear space）是在线性空间中定义了距离（metric）的空间。
距离的定义必须满足如下三个条件：

1. 非负性： $d(x, y) \ge 0; d(x, y) = 0 \Leftrightarrow x = y$ 。
2. 对称性： $d(x, y) = d(y, x)$ 。
3. 三角不等式：$d(x, z) + d(z, y) \ge d(x, y)$ 。

线性赋范空间

线性赋范空间（normed linear space）是定义了范数（norm）的线性度量空间。
范数的定义必须满足：

1. 非负性：$\lVert x \rVert \ge 0$ 。
2. 齐次性：$ \lVert \alpha x \rVert = |\alpha| \lVert x \rVert $ 。
3. 三角不等式：$\lVert x \rVert + \lVert y \rVert \ge \lVert x+y \rVert$ 。

由范数可以导出距离（定义 $d(x, y) = \lVert x - y \rVert$ ），但是不可以由距离导出范数。

巴拿赫空间

巴拿赫空间（Banach space）是完备的赋范线性空间。
完备性（completeness）：任一柯西序列（Cauchy sequence）都收敛（convergence）。

内积线性空间

内积线性空间（inner product linear space）是定义了内积（inner product）的赋范线性空间。
其中内积也叫标量积（scalar product）或点积（dot product）。
这里要注意，内积的定义跟范数其实没关系，不过内积可以导出范数，所以一般内积空间都有范数。
内积的定义必须满足：

1. 对称性：$\langle x, y \rangle = \langle y, x \rangle$ 。
2. 线性性： $\langle x, y \rangle + \langle x, z \rangle = \langle x, y + z \rangle$ 、 $\langle \alpha x, y \rangle = \alpha \langle x, y \rangle$ 。注意：数乘只对第一变元有效。
3. 正定性：$\langle x, x \rangle \ge 0$ 。

由内积可以导出范数（定义 $\lVert x \rVert^{2} = \langle x, x \rangle$ ），但是范数不可以导出内积。

欧几里得空间

欧几里得空间（Euclidean space）是有限维的实内积线性空间。

希尔伯特空间

希尔伯特空间（Hilbert space）是完备的内积线性空间。

两个例子

1. 泰勒级数展开（Taylor series）：将一个函数用 $\lbrace x^{i} \rbrace_{0}^{\infty}$ 作为基底表示的一个空间。
2. 傅里叶级数展开（Fourier series）：将一个函数用 $\lbrace 1, \cos x, \sin x, \cos 2x, \sin 2x, \cdots \rbrace$ 作为基底表示的一个空间。

核函数

终于到主题了，写的手都酸了……

一般的欧式空间中，我们可以定义一个 $n \times n$ 矩阵的特征值和特征向量。

$$Ax=\lambda x$$

考虑一个矩阵的列空间，当这个矩阵可以进行特征值分解的时候，其特征向量就构成了这个 $n$ 维空间的一组基底。

现在我们把这个概念推广到函数空间。

我们把每个函数 $f(x)$ 看作一个无穷维的向量，然后定义一个函数空间中无穷维的矩阵 $K(x, y)$ ，如果它满足：

1. 正定性：$\forall f \rightarrow \iint f(x)K(x, y)f(y) \,\mathrm{d}x\,\mathrm{d}y \ge 0$ 。
2. 对称性：$K(x, y) = K(y, x)$ 。

我们就把它称作核函数（kernel function）。

和特征值与特征向量的概念相似，存在特征值 $\lambda$ 和特征函数 $\psi(x)$ 。满足：

$$\int K(x, y)\psi(x) \mathrm{d}x = \lambda \psi (y)$$

对于不同的特征值 $\lambda_{1}$ 、 $\lambda_{2}$ ，对应不同的特征函数 $\psi_{1}(x)$ 、 $\psi_{2}(x)$ ，很容易得到：

$$\begin{aligned} \int \lambda_1 \psi_{1}(x) \psi_{2}(x) \mathrm{d}x &= \iint K(y, x) \psi_{1}(y) \mathrm{d}y\,\psi_{2}(x)\mathrm{d}x \\ &= \iint K(y, x) \psi_{2}(x) \mathrm{d}x\,\psi_{1}(y)\mathrm{d}y \\ &= \int \lambda_2 \psi_{2}(y) \psi_{1}(y) \mathrm{d}y \\ &= \int \lambda_2 \psi_{2}(x) \psi_{1}(x) \mathrm{d}x \end{aligned}$$

因此，

$$\langle \psi_{1}, \psi_{2} \rangle = \int \psi_{1}(x) \psi_{2}(x) \mathrm{d}x = 0$$

所以我们找到了一个可以生成这个空间的矩阵 $K$，一组无穷多个特征值 $\lbrace \lambda_{i} \rbrace_{i=1}^{\infty}$ ，和一组无穷多个元素的正交基 $\lbrace \psi_{i} \rbrace_{i=1}^{\infty}$ 。

再生核希尔伯特空间

如果我们把 $\lbrace \sqrt{\lambda_{i}}\psi_{i} \rbrace_{i=1}^{\infty}$ 当成一组正交基来生成一个希尔伯特空间 $\mathcal{H}$ 。则该空间中的所有函数都能表示为这组正交基的线性组合。

$$f = \sum_{i=1}^{\infty} f_{i}\sqrt{\lambda_{i}}\psi_{i}$$

于是我们就可以把函数 $f$ ，看作 $\mathcal{H}$ 中的一个向量 $f = (f_{1}, f_{2}, \cdots)_{\mathcal{H}}^{\mathsf{T}}$ 。
对于另外一个函数 $g = (g_{1}, g_{2}, \cdots)_{\mathcal{H}}^{\mathsf{T}}$ ，我们有：

$$\langle f, g \rangle_{\mathcal{H}} = \sum_{i=1}^{\infty}f_{i}g_{i}$$

有了这个内积，我们就可以把核函数看成一种内积形式了，即：

$$K(x, \cdot) = \sum_{i=0}^{\infty} \lambda_{i}\psi_{i}(x)\psi_{i}(\cdot)$$

如果把 $\psi_{i}$ 当成一个算子来看的话，我们就取函数名的一个形式：$K(x, \cdot) = \sum_{i=0}^{\infty} \lambda_{i}\psi_{i}(x)\psi_{i}$ 。
所以我们就可以把 $K$ 当作一个向量来看了。

$$K(x, \cdot) = (\sqrt{\lambda_{1}}\psi_{1}(x), \sqrt{\lambda_{2}}\psi_{2}(x),\cdots)_{\mathcal{H}}^{\mathsf{T}}$$

因此，

$$\langle K(x, \cdot), K(y, \cdot) \rangle_{\mathcal{H}} = \sum_{i=0}^{\infty} \lambda_{i} \psi_{i}(x) \psi_{i}(y) = K(x, y)$$

这个性质就叫再生性（reproducing），这个 $\mathcal{H}$ 就叫做再生核希尔伯特空间（reproducing kernel Hilbert space，RKHS）。

回到我们最初的问题，怎么把一个点映射到一个特征空间上呢？

定义一个映射：

$$\Phi(x) = K(x, \cdot) = (\sqrt{\lambda_{1}}\psi_{1}(x), \sqrt{\lambda_{2}}\psi_{2}(x),\cdots)_{\mathcal{H}}^{\mathsf{T}}$$

则

$$\langle \Phi(x), \Phi(y) \rangle_{\mathcal{H}} = \langle K(x, \cdot), K(y, \cdot) \rangle_{\mathcal{H}} = K(x, y)$$

虽然我们不知道这个映射的具体形式是什么，但是我们可以知道对于一个对称的正定函数（矩阵） $K$ ，一定存在一个映射 $\Phi$ 和一个特征空间 $\mathcal{H}$ ，使得

$$\langle \Phi(x), \Phi(y) \rangle_{\mathcal{H}} = K(x, y)$$

这就叫做核方法（kernel trick）。

所以为什么一个核函数都对应一个正定矩阵呢，就是因为它把核函数看成张成某个 RKHS 的空间的一组基底的线性组合。

在 SVM 中的应用

简单说几句，公式太难写了（笑）。

我们在使用原始数据 $x$ 的时候发现数据并不可分，所以就寄希望于一个映射 $\Phi(x)$ ，这个映射把低维空间上的数据映射到高维空间，这样数据集就有可能变得可分了。

但是在考虑优化问题的对偶问题时，需要计算 $\langle x_{i}, x_{j} \rangle$ ，请注意到，我们已经把所有的 $x$ 换成了 $\Phi(x)$ ，所以就变成需要计算 $\langle \Phi(x_{i}), \Phi(x_{j}) \rangle$ 。
为了不让计算变得很困难，我们就可以找到一个核函数 $K$ ，满足 $K$ 可以生成 $\Phi$ 所形成的高维空间，这样 $\langle \Phi(x_{i}), \Phi(x_{j}) \rangle$ 就可以简单的用 $K(x_{i}, x_{j})$ 代替了。而 $K$ 往往定义成和 $x$ 的内积有关的式子，这样在低维空间中计算内积就很简单。

如：径向基函数里有 $\lVert x - y \rVert^{2}$ ，展开以后其实就含有两个范数项（注意范数就是内积）和一个内积项。